Rekurencja to Rekurencja. Tutaj nawet google się nie myli.
Rekurencja
Czyli inaczej funkcja wywołująca samą siebie. Robi tak aż do osiągnięcia wartości granicznych – na przykład przy ciągu Fibonacciego, aż do osiągnięcia 1 albo 0. Rekurencja do prostych rzeczy nie należy i wiem, że sprawia ona problemy. Zresztą czytając kod różnych programistów widziałem, że raczej robili wszystko by tylko nie wejść w rekurencje.
Zanim więc przejdziemy do bardziej zaawansowanych tematów, dwa przykłady rekurencji:
public static long factorial(int n)
{
if (n == 0)
{
return 1;
}
return n * factorial(n - 1);
}
public static long fib(int n)
{
// could be n == 0 || n == 1 return n;
if (n == 0)
{
return 0;
}
if (n == 1)
{
return n;
}
return fib(n - 2) + fib(n - 1);
}
Jak widzicie nie jest to jakieś super skomplikowane. Trzeba tylko przestawić swój tok myślowy. Może się wam wydawać, że taki błahe przykłady nic nie wniosą do waszej codziennej pracy. Nic bardziej mylnego. W typowej aplikacji biznesowej rekurencja występuje minimum raz – albo to jest moje własne doświadczenie. Czy to stworzenie menu do aplikacji, czy obliczenie czegoś. Szczerze, nauczcie się jej. Przyda się wam na pewno.
Warto też wiedzieć, że każde wywołanie funkcji powoduje dodanie jej do stosu wywołań (call stack, to właśnie daje wam StackTrace w C# przy wyjątkach oraz okno Call Stack w trakcie debuggowania) funkcji – dokładnie trzymana jest informacja do którego miejsca kod ma przeskoczyć jak skończy wywoływać funkcję. Jeżeli teraz mamy jakiś duży zbiór danych, czy też błędnie napisane warunki wyjścia, przy rekurencji łatwo jest ten stos zatkać. A jak się stos zatyka to dostajemy śliczny StackOverflowException. Dla przykładu, metoda bez warunku wyjścia:
public static string stack_overflow_ex(int n)
{
return stack_overflow_ex(n);
}
Wygeneruje:
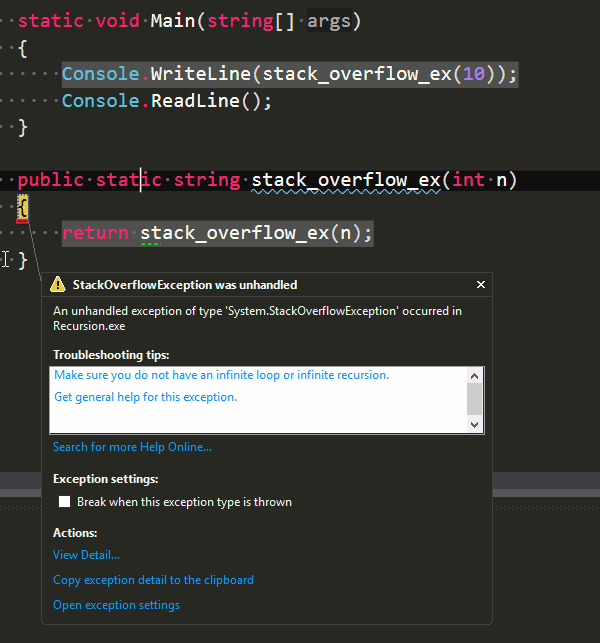
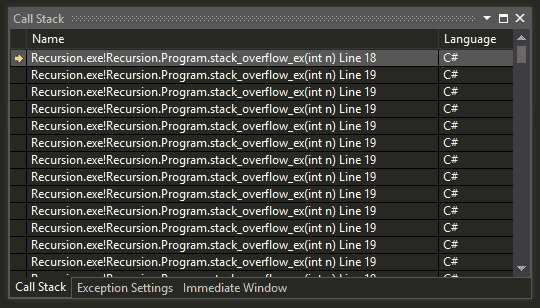
Tail recursion/Rekurencja ogonowa
To skoro wiemy co to jest rekurencja i co powoduje wywołanie funkcji, pora dowiedzieć się co to jest tail recursion a dokładnie tail call, który w szczególnym przypadku zwie się rekurencją ogonową. Tail call to nic innego jak wywołanie funkcji na końcu aktualnej funkcji:
private int method()
{
// …
return tail_call();
}
private int tail_call()
{
return 1;
}
Tail recursion za to, jest to wywołanie tej samej funkcji w której jesteśmy na końcu tej funkcji:
private int tail_recurssion(int someParam)
{
// …
return tail_recurssion(someParam + 1);
}
Dla przykładu Fibbonaci z początku możemy zamienić na wywołanie jedno funkcyjne robiąc z tego tail recursion:
public static long fib(int n, long a, long b)
{
// short: return n == 0 ? b : fib(n - 1, a + b, a);
if (n == 0)
{
return b;
}
return fib(n - 1, a + b, a);
}
Czym to się różni? Tym, że jest tylko jedna metoda na końcu wywoływana – to jest dość ważne.
Teraz, mając tail recursion może zostać zastosowana optymalizacja kodu polegająca na tym, że NIE JEST DODAWANY kolejny stack frame do call stack. By to zademonstrować muszę posłużyć się F#. C# nie posiada optymalizacji tail call. A więc stwórzmy sobie dwie funkcje w F#:
exception BrkError of string
let rec fib_normal n =
match n with
| 0 -> raise(BrkError("see_callstack")) // or 0 and brk point
| 1 -> 1
| n -> fib_normal(n-2) + fib_normal(n-1)
let rec fib_tail (n, a, b) =
match n with
| 0 -> raise(BrkError("see_callstack")) // or b and brk point
| n -> fib_tail(n-1, a+b, a)
Wyrzucam wyjątek bo jest tak łatwiej wam to skopiować i wkleić. W razie co, w komentarzu macie podane co można zamiast wywołania wyjątku zrobić. Te dwa kody generują następujące Call Stack:
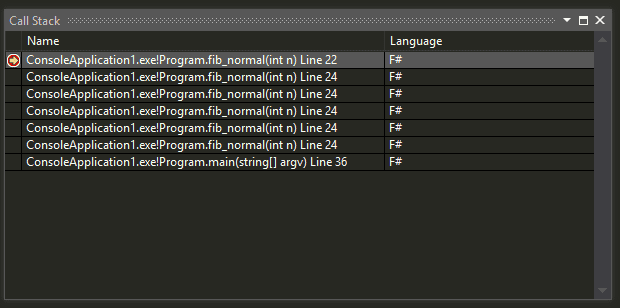
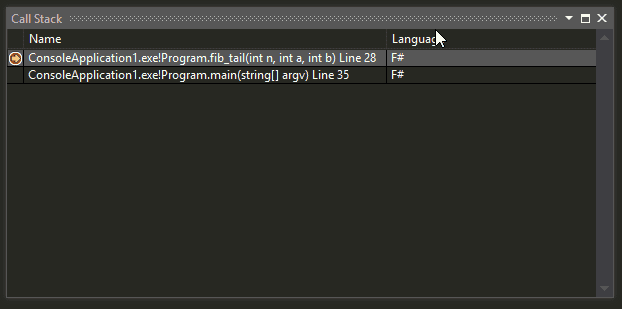
fib_tail. A to znaczy, że nie osiągniemy stack overflow. Wszystko jest stałe, proste. To znaczy, że ze złożoności liniowej O(n) weszliśmy na stałą O(1) (Update 2016-10-26: tak jak Patryk zaznaczył w komentarzu, chodzi o złożoność pamięciową).
Podsumowanie
Wiedza co to jest rekurencja, tail call, rekurencja ogonowa i na czym polega optymalizacja tego jest dość podstawową wiedzą w programowaniu i warto ją posiadać – wiedza już o tym jakiego typu algorytmy są wykorzysytwane do wykrywania tail call to już inna broszka. Chociażby tylko po to by zrozumieć dlaczego coś nam się wysypuje nie wspominając już o językach funkcyjnych, w których bez rekurencji ani rusz. Dodatkowo, rekurencja dość często występuje w programowaniu – możemy tego nie zauważyć gdyż czasami się jej boimy, a nie powinniśmy. A jak się czegoś boimy to szukamy alternatywnej drogi wykonania tego. Następnym więc razem jak będziecie pisali pętle while zastanówcie się czy nie da się tego zrobić za pomocą rekurencji. Po prostu pomyślcie, zastanówcie się, napiszcie ten kod i zobaczcie którą wersję wolicie. Tę zachowajcie a drugą wywalcie z kodu :)
















Rekurencja, szczególnie ogonowa, w językach funkcyjnych jest bardzo ważna. Warto jednak zauważyć, że rekurencja ogonowa w F# jest kompilowana do pętli for albo while. Dlatego otrzymujemy pojedyncze wywołanie funkcji w call stacku.
To zależy. Po pierwsze możesz go zmusić do tego by w debug modę korzystał z tail calls. Do tego wykorzystuje on w il op code tail. Ale tak, ogólne optymalizacja rekurencji ogonowej polega na tym by kod wynikowy był jak najbardziej zbliżony do pętli.
To ciekawe, bo raczej oczekiwał bym optymalizacji przy pomocy goto (imho łatwiej i trochę taniej).
Szkoda tylko, że większość popularnych języków nie wspiera rekurencji ogonowych (Js, C# czy Java).
Polecam zajrzeć jak rozwiązane jest to w Clojure: http://blog.degustudios.com/index.php/2016/05/04/tail-recursion-optimizations/
@Bartłomiej Rogowski
nie wiem dokładnie jak to jest z
tail.op code – w sensie, nie wiem dokładnie jak to potem się przekłada, może to jest potem jeszcze dogototłumaczone.co do pętli, to pętla to…
goto:) więc de facto tak jest. A kiedy jesttail.a kiedygototo nie wiem. Z tego co czytałem, F# użyjetail.jeżeli nie będzie mógł zrobićgoto:źródło
[…] Rekurencja ogonowa i jej optymalizacja […]
“Wszystko jest stałe, proste. To znaczy, że ze złożoności liniowej O(n) weszliśmy na stałą O(1).” – warto dodać, ze chodzi o złożność pamięciową.
True, chodzi o złożoność pamięciową
[…] Rekurencja ogonowa i jej optymalizacja […]
Comments are closed.